Home  ›  What About if It Is Shot Directly Away From the Earth Again Relative to C

What About if It Is Shot Directly Away From the Earth Again Relative to C

Written By domingo, 15 de maio de 2022 Add Comment Edit

Special Relativity

226 Relativistic Addition of Velocities

Learning Objectives

  • Calculate relativistic velocity addition.
  • Explicate when relativistic velocity addition should be used instead of classical addition of velocities.
  • Summate relativistic Doppler shift.

The total velocity of a kayak, similar this one on the Deerfield River in Massachusetts, is its velocity relative to the h2o as well equally the water's velocity relative to the riverbank. (credit: abkfenris, Flickr)

A man with oar in his hand is kayaking downstream in a shallow fast-flowing river.

If you've ever seen a kayak motility down a fast-moving river, you know that remaining in the same place would be hard. The river current pulls the kayak along. Pushing the oars back against the water can move the kayak forward in the water, only that just accounts for function of the velocity. The kayak's move is an example of classical improver of velocities. In classical physics, velocities add together every bit vectors. The kayak's velocity is the vector sum of its velocity relative to the water and the h2o's velocity relative to the riverbank.

Classical Velocity Improver

For simplicity, we restrict our consideration of velocity addition to one-dimensional motion. Classically, velocities add like regular numbers in one-dimensional motion. (See (Effigy).) Suppose, for example, a girl is riding in a sled at a speed one.0 chiliad/s relative to an observer. She throws a snowball first forward, so backward at a speed of 1.5 m/s relative to the sled. Nosotros denote direction with plus and minus signs in one dimension; in this example, forward is positive. Let v be the velocity of the sled relative to the Earth, u the velocity of the snowball relative to the Globe-bound observer, and u\prime the velocity of the snowball relative to the sled.

Classical Velocity Improver

\text{u=v+u}\prime

Thus, when the girl throws the snowball forward, u=1.0 m/s+1.5 m/s=2.5 m/s. It makes good intuitive sense that the snowball volition head towards the Earth-bound observer faster, because it is thrown forward from a moving vehicle. When the girl throws the snowball astern, u=1.0 m/s+\left(-1.5 m/s\right)=-0.5 m/s. The minus sign means the snowball moves abroad from the Earth-spring observer.

Relativistic Velocity Improver

The second postulate of relativity (verified by all-encompassing experimental observation) says that classical velocity addition does non apply to lite. Imagine a car traveling at dark along a straight road, every bit in (Figure). If classical velocity improver applied to light, then the low-cal from the auto's headlights would approach the observer on the sidewalk at a speed \text{u=v+c}. Simply we know that light will motion away from the car at speed c relative to the driver of the car, and calorie-free will move towards the observer on the sidewalk at speed c, also.

According to experiment and the second postulate of relativity, lite from the car's headlights moves away from the car at speed c and towards the observer on the sidewalk at speed c. Classical velocity add-on is not valid.

A car is moving towards right with velocity v. A boy standing on the side-walk observes the car. The velocity of light u primed is shown to be c as observed by the girl in the car and the velocity of light u is also c as observed by the boy.

Showing that the Speed of Light towards an Observer is Constant (in a Vacuum): The Speed of Light is the Speed of Calorie-free

Suppose a spaceship heading straight towards the Globe at one-half the speed of light sends a signal to us on a light amplification by stimulated emission of radiation-produced beam of light. Given that the calorie-free leaves the ship at speed c as observed from the transport, calculate the speed at which it approaches the World.

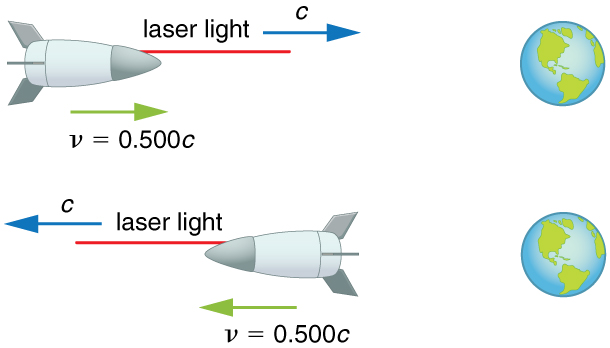
A spacecraft is heading towards earth v equals zero point five zero zero times c. A laser beam from the ship travels towards the Earth with velocity c as shown by a vector. A second spaceship traveling away from the Earth. The velocity of the second ship and second laser are the same as the first, but in the opposite direction.

Strategy

Considering the light and the spaceship are moving at relativistic speeds, we cannot use simple velocity improver. Instead, we can make up one's mind the speed at which the light approaches the Earth using relativistic velocity add-on.

Solution

  1. Identify the knowns. \text{v=}0\text{.}\text{500}c; u\prime =c
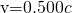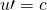
  2. Place the unknown. u
  3. Choose the appropriate equation. u=\frac{\mathrm{v+u}\prime }{1+\frac{vu\prime }{{c}^{2}}}
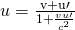
  4. Plug the knowns into the equation.

    \begin{array}{lll}u& =& \frac{\mathrm{v+u}\prime }{1+\frac{vu\prime }{{c}^{2}}}\\ & =& \frac{\text{0.500}c+c}{1+\frac{\left(\text{0.500}c\right)\left(c\right)}{{c}^{2}}}\\ & =& \frac{\left(\text{0.500}+1\right)c}{1+\frac{\text{0.500}{c}^{2}}{{c}^{2}}}\\ & =& \frac{\text{1.500}c}{1+\text{0.500}}\\ & =& \frac{\text{1.500}c}{\text{1.500}}\\ & =& c\end{array}

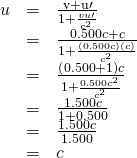
Give-and-take

Relativistic velocity improver gives the correct consequence. Light leaves the ship at speed c and approaches the Earth at speed c. The speed of low-cal is contained of the relative move of source and observer, whether the observer is on the send or Earth-spring.

Velocities cannot add to greater than the speed of light, provided that v is less than c and u\prime does not exceed c. The following case illustrates that relativistic velocity addition is not every bit symmetric every bit classical velocity addition.

Comparison the Speed of Calorie-free towards and away from an Observer: Relativistic Package Delivery

Suppose the spaceship in the previous example is approaching the Earth at one-half the speed of light and shoots a canister at a speed of 0.750c. (a) At what velocity volition an Earth-bound observer see the canister if information technology is shot directly towards the Globe? (b) If it is shot directly away from the Earth? (Come across (Figure).)

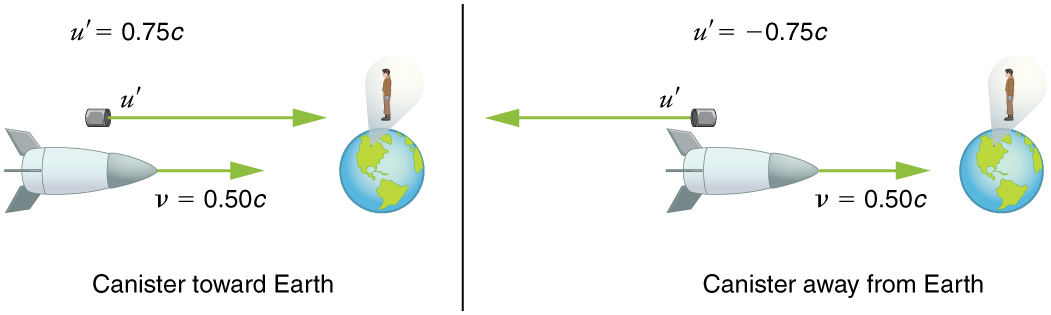
In part a, a spaceship is moving towards the earth from left to right with a velocity v equals to zero point five zero times c. The spaceships shoots a canister towards earth with velocity u prime equals zero point seven five times c. A man stands stationary on earth observing. In part b, the spaceship shoots the canister away from earth with same velocity. In both the cases, the velocity of the ship is v equals 0 point five zero times c toward left.

Strategy

Because the canister and the spaceship are moving at relativistic speeds, we must make up one's mind the speed of the canister by an Earth-spring observer using relativistic velocity improver instead of uncomplicated velocity improver.

Solution for (a)

  1. Identify the knowns. \text{v=}0.500c; u\prime =0\text{.}\text{750}c
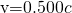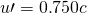
  2. Identify the unknown. u
  3. Choose the appropriate equation. \text{u=}\frac{\mathrm{v+u}\prime }{1+\frac{vu\prime }{{c}^{2}}}
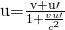
  4. Plug the knowns into the equation.

    \begin{array}{ll}u& =& \frac{\mathrm{v+u}\prime }{1+\frac{vu\prime }{{c}^{2}}}\\ & =& \frac{0.500\text{c +}0.750c}{1+\frac{\left(0.500c\right)\left(0.750c\right)}{{c}^{2}}}\\ & =& \frac{1.250c}{1+0.375}\\ & =& 0.909c\end{array}

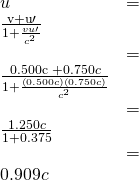
Solution for (b)

  1. Identify the knowns. \text{v}=0.500c; u\prime =-0.750c
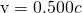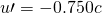
  2. Identify the unknown. u
  3. Cull the appropriate equation. \text{u}=\frac{\mathrm{v+u}\prime }{1+\frac{v\text{u}\prime }{{c}^{2}}}
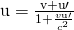
  4. Plug the knowns into the equation.

    \begin{array}{ll}u& =& \frac{\mathrm{v+u}\prime }{1+\frac{vu\prime }{{c}^{2}}}\\ & =& \frac{0.500\mathrm{c +}\left(-0.750c\right)}{1+\frac{\left(0.500c\right)\left(-0.750c\right)}{{c}^{2}}}\\ & =& \frac{-0.250c}{1-0.375}\\ & =& -0.400c\end{array}

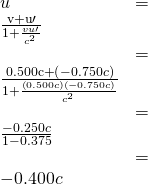
Give-and-take

The minus sign indicates velocity away from the Earth (in the reverse direction from v), which means the canister is heading towards the Earth in part (a) and abroad in part (b), equally expected. Merely relativistic velocities exercise non add as simply as they do classically. In part (a), the canister does approach the Earth faster, but not at the simple sum of 1.250c. The total velocity is less than you would become classically. And in part (b), the canister moves away from the Earth at a velocity of -0.400c, which is faster than the -0.250c yous would await classically. The velocities are not even symmetric. In part (a) the canister moves 0.409c faster than the ship relative to the Globe, whereas in part (b) it moves 0.900c slower than the ship.

Doppler Shift

Although the speed of light does not change with relative velocity, the frequencies and wavelengths of low-cal do. First discussed for audio waves, a Doppler shift occurs in whatever moving ridge when there is relative movement between source and observer.

Relativistic Doppler Furnishings

The observed wavelength of electromagnetic radiation is longer (called a red shift) than that emitted past the source when the source moves away from the observer and shorter (called a blue shift) when the source moves towards the observer.

{\text{=λ}}_{\text{obs}}{\text{=λ}}_{s}\sqrt{\frac{1+\frac{u}{c}}{1-\frac{u}{c}}}.

In the Doppler equation, {\lambda }_{\text{obs}} is the observed wavelength, {\lambda }_{s} is the source wavelength, and u is the relative velocity of the source to the observer. The velocity u is positive for motility away from an observer and negative for motion toward an observer. In terms of source frequency and observed frequency, this equation can be written

{f}_{\text{obs}}{\text{=f}}_{s}\sqrt{\frac{1-\frac{u}{c}}{1+\frac{u}{c}}}.

Notice that the – and + signs are dissimilar than in the wavelength equation.

Career Connection: Astronomer

If you lot are interested in a career that requires a noesis of special relativity, in that location's probably no meliorate connection than astronomy. Astronomers must have into account relativistic effects when they calculate distances, times, and speeds of black holes, galaxies, quasars, and all other astronomical objects. To accept a career in astronomy, you lot need at least an undergraduate degree in either physics or astronomy, but a Principal's or doctoral degree is often required. You lot too need a skilful groundwork in high-level mathematics.

Calculating a Doppler Shift: Radio Waves from a Receding Galaxy

Suppose a galaxy is moving away from the Earth at a speed \text{0.825}c . It emits radio waves with a wavelength of 0\text{.}\text{525}\phantom{\rule{0.25em}{0ex}}\text{m}. What wavelength would we detect on the Earth?

Strategy

Considering the galaxy is moving at a relativistic speed, nosotros must determine the Doppler shift of the radio waves using the relativistic Doppler shift instead of the classical Doppler shift.

Solution

  1. Identify the knowns. \text{u=}0\text{.}\text{825}c ; {\lambda }_{s}=0\text{.}\text{525}\phantom{\rule{0.25em}{0ex}}m
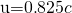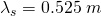
  2. Identify the unknown. {\lambda }_{\text{obs}}
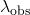
  3. Choose the appropriate equation. {\lambda }_{\text{obs}}{\text{=λ}}_{s}\sqrt{\frac{1+\frac{u}{c}}{1-\frac{u}{c}}}
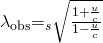
  4. Plug the knowns into the equation.

    \begin{array}{lll}{\lambda }_{\text{obs}}& =& {\text{λ}}_{s}\sqrt{\frac{1+\frac{u}{c}}{1-\frac{u}{c}}}\\ & =& \left(0.525 m\right)\sqrt{\frac{1+\frac{0\text{.}\text{825}\text{c}}{c}}{1-\frac{0\text{.}\text{825}\text{c}}{c}}}\\ & =& \text{1.70 m.}\end{array}

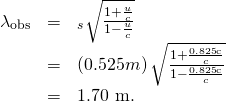
Discussion

Because the milky way is moving away from the Earth, we expect the wavelengths of radiation it emits to be redshifted. The wavelength we calculated is 1.70 m, which is redshifted from the original wavelength of 0.525 m.

The relativistic Doppler shift is easy to observe. This equation has everyday applications ranging from Doppler-shifted radar velocity measurements of transportation to Doppler-radar storm monitoring. In astronomical observations, the relativistic Doppler shift provides velocity information such as the motion and distance of stars.

Bank check Your Agreement

Suppose a space probe moves away from the Earth at a speed 0\text{.}\text{350}c. Information technology sends a radio moving ridge bulletin dorsum to the Earth at a frequency of ane.50 GHz. At what frequency is the message received on the World?

Answer

{f}_{\text{obs}}{\text{=f}}_{s}\sqrt{\frac{1-\frac{u}{c}}{1+\frac{u}{c}}}=\left(1\text{.}\text{50 GHz}\right)\sqrt{\frac{1-\frac{0\text{.}\text{350}\text{c}}{c}}{1+\frac{0\text{.}\text{350}\text{c}}{c}}}=1\text{.}\text{04 GHz}

Section Summary

Conceptual Questions

Explain the meaning of the terms "red shift" and "blue shift" every bit they relate to the relativistic Doppler effect.

What happens to the relativistic Doppler outcome when relative velocity is null? Is this the expected result?

Is the relativistic Doppler effect consistent with the classical Doppler effect in the respect that {\lambda }_{\text{obs}} is larger for motion away?

All galaxies further abroad than about \text{50}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{ly} exhibit a ruby shift in their emitted light that is proportional to distance, with those further and farther away having progressively greater red shifts. What does this imply, assuming that the just source of ruby shift is relative move? (Hint: At these big distances, information technology is infinite itself that is expanding, just the effect on light is the aforementioned.)

Problems & Exercises

Suppose a spaceship heading straight towards the Earth at 0\text{.}\text{750}c can shoot a canister at 0\text{.}\text{500}c relative to the send. (a) What is the velocity of the canister relative to the Earth, if it is shot direct at the Earth? (b) If it is shot directly away from the Earth?

(a) 0\text{.}\text{909}c

(b) 0\text{.}\text{400}c

Echo the previous problem with the send heading direct away from the Earth.

If a spaceship is approaching the World at 0.100c and a message capsule is sent toward information technology at 0.100c relative to the Earth, what is the speed of the capsule relative to the ship?

0\text{.}\text{198}c

If a galaxy moving abroad from the Earth has a speed of 1000 km/s and emits \text{656 nm} light characteristic of hydrogen (the most mutual element in the universe). (a) What wavelength would we observe on the Earth? (b) What blazon of electromagnetic radiations is this? (c) Why is the speed of the Earth in its orbit negligible hither?

a) \text{658 nm}

b) red

c) v/\text{c}=9\text{.}\text{92}×{\text{10}}^{-5} (negligible)

A infinite probe speeding towards the nearest star moves at 0\text{.}\text{250}c and sends radio information at a broadcast frequency of ane.00 GHz. What frequency is received on the Earth?

If two spaceships are heading directly towards each other at 0\text{.}\text{800}c, at what speed must a canister be shot from the first transport to approach the other at 0\text{.}\text{999}c every bit seen by the second send?

0\text{.}\text{991}c

Two planets are on a collision course, heading directly towards each other at 0\text{.}\text{250}c. A spaceship sent from one planet approaches the second at 0\text{.}\text{750}c every bit seen by the second planet. What is the velocity of the ship relative to the get-go planet?

When a missile is shot from 1 spaceship towards another, it leaves the first at 0\text{.}\text{950}c and approaches the other at 0\text{.}\text{750}c. What is the relative velocity of the ii ships?

-0\text{.}\text{696}c

What is the relative velocity of ii spaceships if one fires a missile at the other at 0.750c and the other observes it to approach at 0.950c?

Near the center of our galaxy, hydrogen gas is moving straight abroad from the states in its orbit about a black hole. We receive 1900 nm electromagnetic radiation and know that it was 1875 nm when emitted by the hydrogen gas. What is the speed of the gas?

0\text{.}\text{01324}c

A highway patrol officer uses a device that measures the speed of vehicles past billowy radar off them and measuring the Doppler shift. The approachable radar has a frequency of 100 GHz and the returning repeat has a frequency 15.0 kHz higher. What is the velocity of the vehicle? Notation that there are ii Doppler shifts in echoes. Be certain not to circular off until the finish of the problem, considering the effect is small.

Prove that for whatsoever relative velocity v between ii observers, a beam of light sent from i to the other volition approach at speed c (provided that v is less than c, of grade).

u\prime \phantom{\rule{0.25em}{0ex}}=c, then

\begin{array}{ll}u& =& \frac{\text{v+u}\prime }{1+\left(\text{vu}\prime /{c}^{2}\right)}=\frac{\text{v+c}}{1+\left(\text{vc}/{c}^{2}\right)}=\frac{\text{v+c}}{1+\left(v/c\right)}\\ & =& \frac{c\left(\text{v+c}\right)}{\text{c+v}}=c\end{array}

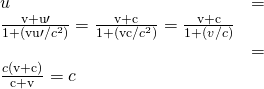
(a) All only the closest galaxies are receding from our own Galaxy Galaxy. If a galaxy \text{12}\text{.}0×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{ly} ly away is receding from the states at 0.0.900c, at what velocity relative to us must nosotros send an exploratory probe to approach the other galaxy at 0.990c, as measured from that galaxy? (b) How long volition it take the probe to accomplish the other galaxy every bit measured from the Earth? You may assume that the velocity of the other galaxy remains constant. (c) How long will information technology then take for a radio signal to be beamed back? (All of this is possible in principle, but not practical.)

a) 0\text{.}\text{99947}c

b) 1\text{.}\text{2064}×{\text{10}}^{\text{11}}\phantom{\rule{0.25em}{0ex}}\text{y}

c) 1\text{.}\text{2058}×{\text{10}}^{\text{11}}\phantom{\rule{0.25em}{0ex}}\text{y} (all to sufficient digits to prove furnishings)

gregorylovent.blogspot.com

Source: https://opentextbc.ca/openstaxcollegephysics/chapter/relativistic-addition-of-velocities/

Related Posts

0 Response to "What About if It Is Shot Directly Away From the Earth Again Relative to C"

Postar um comentário

Assinar: Postar comentários (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel